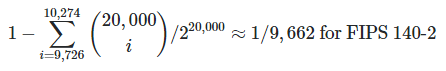Understanding Dieharder, Chi-Square, FIPS-140-2 Results
We have received a number of emails on the performance testing of the TrueRNG. Every one of these have ultimately been attributed to a small sample size or incorrect testing.
The TrueRNG products generate true random numbers – there is no guaranty that chi-squared or other statistical tests will fall within any given range for a small sample size.
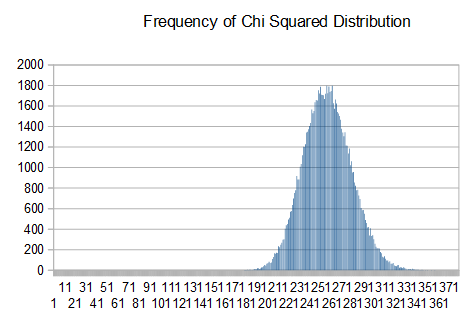
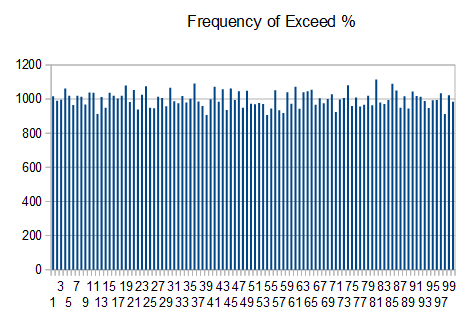
To show this, I captured a large number of 10k blocks from the TrueRNG and ran the ‘ent’ tool on each one and captured the results. I then imported them into Openoffice Calc and did a frequency distribution on the chi-squared distribution and exceed percent values
Here are plots of the results
The Openoffice Calc spreadsheet is here. Here is the source data.
Notice that the chi-squared values follow a normal distribution centered around 256 and that the exceed percent values have a uniform distribution. For a large number of runs, this is the expected result.
From this, you can see that taking a small number of tests from a small sample size may give results that ‘seem’ bad. With a perfect generator, it is expected to get percent values < 5 or > 95 in 10% of the results. If you don’t see this distribution over a large number of runs, then there may be an issue.
It is expected that a true random number generator will fail statistical tests a certain percentage of the time.
For example, typical results from rngtest tool which runs FIPS 140-2 tests are:
Copyright (c) 2004 by Henrique de Moraes Holschuh
This is free software; see the source for copying conditions. There is NO warranty; not even for MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.
rngtest: starting FIPS tests...
rngtest: entropy source drained
rngtest: bits received from input: 114688000000
rngtest: FIPS 140-2 successes: 5729915
rngtest: FIPS 140-2 failures: 4484
rngtest: FIPS 140-2(2001-10-10) Monobit: 595
rngtest: FIPS 140-2(2001-10-10) Poker: 548
rngtest: FIPS 140-2(2001-10-10) Runs: 1653
rngtest: FIPS 140-2(2001-10-10) Long run: 1708
rngtest: FIPS 140-2(2001-10-10) Continuous run: 0
rngtest: input channel speed: (min=1713062.099; avg=9994464560.376; max=0.000)bits/s
rngtest: FIPS tests speed: (min=1.557; avg=82.152; max=85.531)Mibits/s
rngtest: Program run time: 1343537517 microseconds
Notice that there are 5729915 successes and 595 Monobit failures (out of 5734399 runs). For FIPS 140-2, the monobit test is EXPECTED to fail about 1 out of every 9662 runs with a perfect random source.
For 5,734,339 runs, we would expect about 593.5 failures which is very close to the actual number of failures of 595. Similarly, a certain number of failures is expected for each of the tests (except for the continuous run obviously).
Notes on other failures
For Dieharder, using the correct options and having sufficient input data is very important. You need 14+ gigabytes of input data to run dieharder with a small number of rewinds. Having a small data file input feeds the same data multiple times into the test and often gives false ‘FAILED’ results. I run most dieharder tests with:
dieharder -g 201 -k 2 -Y 1 -f FILENAME-g 201 = use external file as input
-k 2 = use maximum accuracy to machine precision (slower)
-Y 1 = resolve ambiguity mode = reruns ‘WEAK’ results until PASSED or FAILED result is obtained
-f FILENAME = the name of the file to use for the source
diehard_sums test
Other dieharder failures
As with other statistical tests for random number generators, it is expected that each dieharder test gets a ‘FAILED’ result a certain percentage of the time.
A single of small number of failures on a particular test is not a cause to label the generator as bad. For a ‘FAILED’ result, a particular test can be re-ran on the same input file with a larger block size to show that the failure is an anomaly.
I use the following to re-run a single particular dieharder test and increase the p_value multiplier (-m) and/or use split to chop up the input file into chunks then test each one separately (re-running the same test on the same input will get the same result and not tell you anything about the rest of the file)
dieharder -d 201 -g 201 -k 2 -Y 1 -m 2 -f FILENAME-d 201 = test number to run — see below
-g 201 = use external file as input
-k 2 = use maximum accuracy to machine precision (slower)
-Y 1 = resolve ambiguity mode = reruns ‘WEAK’ results until PASSED or FAILED result is obtained
-m 2 = use twice the number of p_samples as input
-f FILENAME = the name of the file to use for the source
Dieharder Test Flags
-d 0 Diehard Birthdays Test Good
-d 1 Diehard OPERM5 Test Good
-d 2 Diehard 32x32 Binary Rank Test Good
-d 3 Diehard 6x8 Binary Rank Test Good
-d 4 Diehard Bitstream Test Good
-d 5 Diehard OPSO Suspect
-d 6 Diehard OQSO Test Suspect
-d 7 Diehard DNA Test Suspect
-d 8 Diehard Count the 1s (stream) Test Good
-d 9 Diehard Count the 1s Test (byte) Good
-d 10 Diehard Parking Lot Test Good
-d 11 Diehard Minimum Distance (2d Circle) Test Good
-d 12 Diehard 3d Sphere (Minimum Distance) Test Good
-d 13 Diehard Squeeze Test Good
-d 14 Diehard Sums Test Do Not Use
-d 15 Diehard Runs Test Good
-d 16 Diehard Craps Test Good
-d 17 Marsaglia and Tsang GCD Test Good
-d 100 STS Monobit Test Good
-d 101 STS Runs Test Good
-d 102 STS Serial Test (Generalized) Good
-d 200 RGB Bit Distribution Test Good
-d 201 RGB Generalized Minimum Distance Test Good
-d 202 RGB Permutations Test Good
-d 203 RGB Lagged Sum Test Good
-d 204 RGB Kolmogorov-Smirnov Test Test Good
-d 205 Byte Distribution Good
-d 206 DAB DCT Good
-d 207 DAB Fill Tree Test Good
-d 208 DAB Fill Tree 2 Test Good
-d 209 DAB Monobit 2 Test Good
If there is consistent failure on a particular test using multiple input runs and the test is not suspect, then there may be something wrong with the random number generator or testing methodology.